ふくほのひとりごと。

高専生が勉強したことの自分用メモ。

正弦波っぽい放物線をフーリエ級数展開して遊んだ話

ふくほです。
またまた久しぶりの記事になってしまった。

今回は，放物線をふたつ組み合わせた，めっちゃ正弦波っぽいグラフをフーリエ級数展開したらどうなるかを考えてみました。

きっかけ

高専1年生で初めて正弦波を見たとき，放物線の合成にしか見えませんでした。
ただ，話によると正弦波と放物線は全く別物。まじ？
そのだいぶ後に単位円の話を聞いて，放物線と無関係であることは納得したのですが，やはり形が似ているような……。

ここで，割と最近知ったフーリエ級数の話。周期関数を三角関数の和の形で表すというものです。
放物線をフーリエ級数展開すると面白いことになりそう！
ということで，やってみました。

今回は遊んだだけなので，手計算はせずにwolframとpythonに頼りきって演算をしました。

準備する放物線

y =\sin{x}に似た放物線として，以下のような放物線を用意しました。
Parabola1 : y = -\dfrac{4}{\pi^2}(x-\dfrac{\pi}{2})^{2} + 1\\ Parabola2 : y = \dfrac{4}{\pi^2}(x-\dfrac{3\pi}{2})^{2} - 1
グラフにするとこんな感じ↓
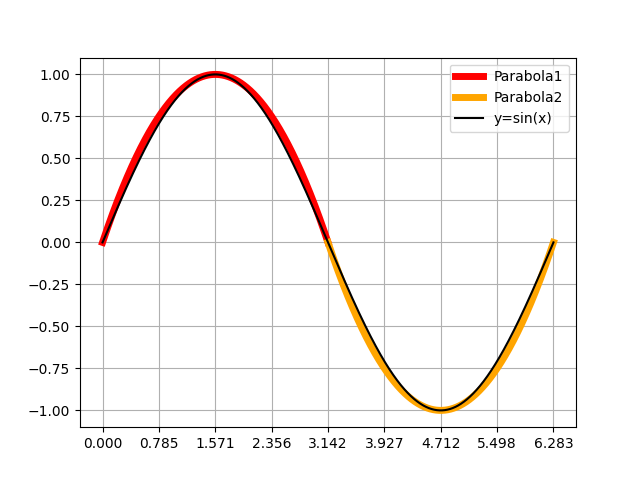
f:id:fukuro_hoho:20211204133752p:plain
正弦波と重ねてみても似ていることがわかります。
まあ，ちょっと放物線の方が広がってる感じするけど……。

放物線は，頂点の座標とx軸との交点の座標から決めました。

フーリエ級数展開してみる

それでは，前の放物線の組み合わせを周期 2\piの周期関数としてフーリエ級数展開してみます。
y \sim c_{0} + \sum_{n=1}^{\infty}(a_{n}\cos{nx}+b_{n}\sin{nx})
フーリエ級数展開については記事を書いたことがあるので，貼っておきます。
fukuro-hoho.hatenablog.com

今回は1周期の積分値が0になるのはグラフから明らかなので， c_0=0となります。
また，この関数は奇関数となるため， a_n = 0が任意の1以上のnについて言えます。

さて，残りの b_nですが，これは手計算は面倒なのでwolfram alphaに投げました……。
計算結果はこんな感じ。
b_n = \dfrac{16}{(n\pi)^3} (1 - (-1)^{n})

nが偶数の時 b_nは0となり，奇数以外の時はb_n = \dfrac{32}{(n\pi)^3}になるみたいです。

www.wolframalpha.com

求まったb_nを， n=1から順にグラフにしてみると，こうなりました。
f:id:fukuro_hoho:20211204141028p:plain
え……すご。 n=1ではほぼ1になっていますが，それ以外での値はほぼ0になっています。
主成分以外の周波数成分はほとんど含まれてないんですね。
ちなみに，数値を出力させるとこんな感じ。
f:id:fukuro_hoho:20211204141645p:plain
n =1の時しかほぼ値がないといった感じ。
この値は，前の式から n^{3}に反比例するので，かなりの速さで0に収束していきます。

うわ～～，すごい……。
これだと，放物線と正弦波を初見で同じだと感じるのも仕方がなさそうです。(多分)
本当に感動して一晩寝るのに苦労しました。

思い切ってソースコードを公開しちゃう

今回は手計算なしで，すべてpythonとwolframに投げたという話をしました。
ありふれたことしか書いていませんが，pythonのコードをせっかくなので公開しておきます。

まず，1枚目のグラフを描いてくれたプログラムから。

import math
from matplotlib import pyplot as plt
import numpy as np

# 横着者なので
pi = math.pi
def sin(x):
    return np.sin(x)

x1 = np.linspace(0,pi,10000)
x2 = np.linspace(pi,2*pi,10000)
x = np.linspace(0,2*pi,20000)

y1 = -4 / (pi*pi) * (x1 - pi/2)*(x1 - pi/2) + 1
y2 = 4 / (pi*pi) * (x2 - 3*pi/2)*(x2 - 3*pi/2) - 1

plt.plot(x1,y1,lw = 5,color = 'red',label = 'Parabola1')
plt.plot(x2,y2,lw = 5,color = 'orange',label = 'Parabola2')
plt.plot(x,sin(x),color = 'black',label = 'y=sin(x)')
plt.xticks(np.linspace(0,2*pi,9))
plt.grid()
plt.show()

次に，各 nに対してフーリエ係数を求め，グラフを出力してくれるプログラム。

import math
from matplotlib import pyplot as plt
import numpy as np

# 横着者なので
pi = math.pi
def pow(x,n):
    ans = 1
    for i in range(n):
        ans *= x
    return ans
def cos(x):
    return np.cos(x)

n = np.linspace(1,21,11)
b = (16 / pow(n*pi,3)) * (1 - 1 * cos(n*pi))

cnt = 1
for i in b:
    # 出力をそろえる
    if cnt < 10:
        print('n :', cnt, '   b_n :', i)
    else:
        print('n :', cnt, '  b_n :', i)
    cnt += 2

plt.xticks(np.arange(1,22,2))
plt.plot(n,b,color = 'red')
plt.grid()
plt.show()

最後に

長年のモヤモヤがすっきりしてうれしいです。
ただ，記事を書くことを試験期間中に思い立ってしまったことだけが反省点。今回の試験範囲にフーリエ級数展開の話があったし，これで試験勉強したってことにならないかなぁ……。(多分ならない)