ふくほのひとりごと。

高専生が勉強したことの自分用メモ。

大学編入試対策としてやったこと

ふくほです。
高専5年生になり大学編入試を受けました。以前は時系列で記事を書きましたが，今回は科目別・使った参考書別に記事を纏めようと思います。(前の記事では具体的に何を使ったのかを書いていませんでした)おそらくこれから編入を控えている高専生の方々にとっては，以前投稿した体験記よりもこっちの記事の方が有益です。まあ，もしよかったら体験記も読んでみてください。↓
fukuro-hoho.hatenablog.com


私が編入試で対策したのは数学，物理，化学，英語です。これから，科目ごとに使った参考書などを書いていこうと思います。

勉強を始めた時期

勉強を始めた時期ですが，3年生の春というのが一番正確な気がします。というのは，ずっと編入試のことは考えていたのですが，1, 2年生の時は体調不良が続いておりきちんとした勉強ができていなかったので……。勉強してるといっても，ちょっとカフェで授業の予習をしたり，趣味で高校数学の参考書を読んだりする程度でした。これは受験勉強とはいえません。

数学

共通数学

まず，どこでも出してくるであろう数学です。のちに応用数学のことも書くので，ここでは共通数学と書きます。共通数学はどこの大学でもあるし，3年生で習う微積・線形代数をひねった問題が多いので，早めから対策しやすいです。

私がメインで使ったのはこれです。大学編入への数学問題集。
amzn.asia
大学編入界隈ではかなりメジャーな問題集です。大問数は応用数学合わせて270。難易度がA,B,Cに分けられており，C問題になると東大の問題とかが平気で出てきます。私はあまり読まなかったのですが，解説も分厚くおすすめです。私は2年生の終わりごろに買って，3年生のオンライン授業中(前期ほとんどオンラインだったので)に解いたりしていました。すぐ解ける問題は眺めるだけとかにしていましたが，手ごたえのある問題は7,8周しました。

私が愛用した微積の参考書として，これも挙げておきます。(実教出版の微積II)
www.amazon.co.jp
3年生の数学の授業の教科書でした。ロピタルの定理の証明とか，微積分の根本的な考え方が丁寧に書かれているのでとてもよいです。私は5年生になってからこの本の魅力に気づき，数学の根本を理解することに努めました。

次はこれです。(編入数学過去問特訓)
www.amazon.co.jp
徹底研究(後述)を仕上げた人をターゲットにしてるっぽいです。これも大学編入のための数学問題集と同様，問題の難易度がA,B,Cに分けられています。C問題は，そこそこの難易度です。私は，5年生になる前の春休み(4年生の3月)に購入し，とりあえずわからない問題がなくなるまで解きました。かなり手ごたえがあります。

また，マセマシリーズがわかりやすいと聞いたことがあったので読み込みました。かなりわかりやすいし，よくまとまっているのでお勧めです。特に常微分方程式。統計学は，お気持ち程度でいいかも。

(マセマ線形代数)

(マセマ 常微分方程式)
https://www.amazon.co.jp/%E5%B8%B8%E5%BE%AE%E5%88%86%E6%96%B9%E7%A8%8B%E5%BC%8F%E3%82%AD%E3%83%A3%E3%83%B3%E3%83%91%E3%82%B9%E3%83%BB%E3%82%BC%E3%83%9F-%E6%94%B9%E8%A8%828-%E9%A6%AC%E5%A0%B4-%E6%95%AC%E4%B9%8B/dp/4866152192/ref=d_pd_vtp_sccl_2_4/357-5047108-7252804?pd_rd_w=at9HD&content-id=amzn1.sym.cbb45385-7b99-44b7-a528-bff5ddaa153d&pf_rd_p=cbb45385-7b99-44b7-a528-bff5ddaa153d&pf_rd_r=AWK2W5WDXNVM0Z8H1AW2&pd_rd_wg=Zv88h&pd_rd_r=b5271625-0a7b-46e2-b14e-aefd44ef40a0&pd_rd_i=4866152192&psc=1

(マセマ 確率統計)

本以外にも，Twitterに数学に詳しい方がたくさんいらっしゃるので，よく教えてもらっていました。


また，私は買っていないけど編入界隈でメジャーなものものせておきます。
まず徹底研究。

www.amazon.co.jp
大学編入のための数学問題集かどっちかでいいと思います。また，徹底研究が難しく感じた人は，編入数学入門っていうのがいいらしいです。私は持ってません。

www.amazon.co.jp

徹底研究に関連して，最近微積に特化した徹底研究と，線形代数に特化した徹底研究が出たそうです。パラっと見たことしかありませんが，丁寧そうでした。(どっちも持ってないけど)
www.amazon.co.jp
www.amazon.co.jp



応用数学

応用数学は，大阪大学の入試(数理科学コースの専門科目)で使いました。大きく分けてベクトル解析，複素関数論，フーリエ解析の3つがあります。
まずは教科書をたくさん読んで，付属の問題集を何周かしました。(教科書↓)
www.amazon.co.jp
付属問題集，応用問題として普通に東大の問題を載せてきたりして面白かったです。


また，あまり本質的な理解が得られていない気がしたので，Twitterの方々とゼミをしました。複素関数論のゼミと，フーリエ解析のゼミの2つでした。使った本を載せておきます。
ただ，私が参加したゼミは工学部への編入対策としては難しすぎだった気もするので，学校で応用数学の授業があるならその付属問題集だけで充分足りると思います。

(神保複素関数入門)
www.amazon.co.jp

www.amazon.co.jp


また，独学用にと思いマセマを購入しました。かなりおすすめです。

(マセマ複素関数)


物理

編入試験の物理では，初等力学，電気磁気学，熱力学が頻出です。私は熱力学はないので(阪大にあったけど，力学と電磁気を取れば解かなくてよかったので)何もしていません。

初等力学

まずは，高専生に好かれているこの本です。

(大学生の初等力学)

大学生の，といいつつもかなり高専生に扱いやすい内容・解説になっています。私はこれを3年生の終わりくらいに買って，ゆっくり回しました。なかなか解けない問題は十数回解いたと思います。私が持ってるのは改訂版じゃないやつです。

続いて，理論をしっかり勉強するのにおすすめの本がこれです。

(基幹講座 力学)

学部低学年を対象に書かれているらしく，ある程度の微積・線形代数の知識があればすっと理解できるいい本です。京大を受験することを考えているなら，この本で保存力の証明といった理論的なところも詰めていくといいと思います。この本には本当に出会ってよかったなぁと思っています。発展のところも読むとかなり面白いし。

私が使ったのはこの2冊だけです。あとは学校の試験(応用物理って科目)の予想問題を定期試験前に3周くらいしてたので，基本問題は手が勝手に動くようになってました。


電気磁気学

初等力学に続き，電磁気もこの本がおすすめです。

(大学生の電磁気学)

最近手に入れることすら難しくなってるみたいですね……めっちゃ高い。
この本は内容はすごくいいのですが，誤植がかなり多いので正誤表が見られるリンクも貼っておきます。

弱点克服 大学生の電磁気学

また，あまり使ってませんがサブでこの本も買いました。

(電磁気学演習 (理工基礎物理学演習ライブラリ))

これはちょっと難しいかな～という印象でした。院試にも使えると聞いて頑張って演習したのですが，情報系の院試に電磁気がないことに最近気づいて虚無い。
とはいえ，ガウスの定理とか鏡像法とかのパターンに縛られない万能な使い方を教えてくれるのでかなりいい本だとは思います。初見でいきなり解くのはお勧めできませんが…。

あとは，学校の授業で使った教科書と，隣の電気工学科が使ってる教科書(もらい物)を持っているので，気になることがあればぺらぺらしていました。一応リンクも貼っときます。

電気磁気学 (電気学会大学講座) | 直平, 山田, 誠, 桂井 |本 | 通販 | Amazon

電磁気学 | 亨, 宇野, 宏, 白井 |本 | 通販 | Amazon


化学

私が受けた中では京大でのみ試験がありました。化学はやる気が出ず，かなり後回しにしてしまいましたが，4年の3月時点でまあまあ余裕があったので始めました。化学を捨てて受かっている人は多いですが，京大では化学の配点は物理と同じとまあまあ高いため，数学でちょっとミスをした時のカバーに使えるためやっておいた方がいいです。私は多分化学捨ててたら落ちてたので……。

理論化学

まずこれ。

(大学への橋渡し 一般化学)

先輩方が推していたので同じやつ買いました。良いです。章末問題は4周くらい回しました。解答は公式がHPに載せてます。結合軌道とかの話は，ヨビノリの動画が最高にわかりやすいです。私は最後の方全部スクショして試験前日まで見てました。混成軌道の話とかは編入試に出しやすいしそんなに難しくないので，しっかりやっておくといいかもしれません。

youtu.be

無機化学

院試とかにも使えそうな演習問題集とかを買ってみましたが，編入試で出そうな難易度は一般化学でカバーできていたのでやめました。理論化学と無機化学の違い，よくわからん……。
R3年の京大の編入試には高校化学ちっくなイオンの色の問題が多く出題されていましたが，あのあたりはどうやってカバーしたらいいかわからなかったので諦めました。炎色反応だけ，地元の花火大会の時に花火と炎色反応の色一覧を交互に見て覚えました。実物を見ながらだと覚えやすいのでおすすめです。花火綺麗だし。

有機化学

強敵！！私は春休みにとりあえずこれを頑張りました。

(困った時の有機化学 上下)

上巻は12章以外はほぼ全部，下巻は1, 4, 5章を読み，暗記シートを作って覚えました。特に芳香族は京大が出しがちなので入念に対策しました。私の年は出なかったけど。
先輩でマクマリーを使っている方が多いのですが，話によると概説でもまあまあ難しいし頭に入ってきにくいらしいのでこれを使いました。過去にこの本で京大合格した方もいらっしゃるらしいので。

また，本だけだとあまり面白くないので，YouTubeでもろぴーの解説動画をお昼ご飯を食べながら見たりしていました。1本が短いので見やすいし，わかりやすくておすすめです。

www.youtube.com

最後に演習問題集も買いました。

(有機化学演習 基本から大学院入試まで)
www.amazon.co.jp

凄く高かった……あとすごく難しかった……非化学系がいきなり攻めるとつらいので，まずは例題を電車の中で読むとかするといいと思います。私は6章までを2周だけ解いて，あとは読んでました。


わからないことがあったらTwitterの化学系の方に質問し教えてもらっていました。おかげさまで……本番の有機化学は8割くらい分かった気がします，感謝。

物理化学

熱力学と化学電池とかの分野が合わさってる感じなのが物理化学という認識です。私はとりあえずこれを使いました。

(単位の取れる物理化学ノート)

この本を買おうとしたとき，電子書籍でめっちゃポイントが返ってくるキャンペーンをやっていたので電子書籍で買い，iPadで読んでいました。わかりやすいし深さもちょうどいいと思います。京大は，クラウジウス・クラペイロンの式みたいな複雑に見えるような式は説明問題で出してくる傾向にあるので，暗記よりも説明重視で勉強しました。

そしてどうしても外せないのが，やっぱりヨビノリ。熱力学の連続講義もあり，2, 3周しました。

www.youtube.com

あともう1つ，わかりやすいYouTubeチャンネルがあったので，それも載せておきます。

www.youtube.com

このチャンネルはかなりわかりやすいし，板書の見やすさ最高なのでスクショしてたくさん見てました。

英語

中学時代に英語が得意だったので，ずっとさぼってました……。帰国子女とかじゃないのに……。とりあえず，単語は肝なので忘れないようにと，大事な試験の前(TOEICとかTOEFLとか)には鉄壁をQuizletで詰め込んでました。

www.amazon.co.jp

かなり網羅性がよく，難易度もそこそこなので重宝しています。これからも使おうと思います。

京都大学の編入試では，英語がTOEFLのスコアに置き換えられます。TOEFLはSpeakingやWritingで人間の採点者もいるからか，245米ドル(米ドル固定なので，円安が加速すると最悪)と受験料がかなり高く，何度も受けられる試験ではありません。一度でなるべくいいスコアとる気持ちで頑張りました。
まず使ったのが単語帳。TOEFLはアカデミックな話題が多く出題されるため，鉄壁だけでは足りません。ここでアルクの単語帳を買いました。(英検でお世話になっていたので圧倒的信頼感がありました)

www.amazon.co.jp

アルクの単語帳はすごく見やすく使い勝手が良いので，英検を受けるときも度々お世話になっていました。とりあえず3800単語を詰め込みました。
演習問題はこれを使いました。

www.amazon.co.jp

買った理由は簡単で，ジュンク堂に行ったときにあった中で一番コスパがよかったからです。初めてこれを解いた時，TOEFLの問題形式にめっちゃ驚いたのを覚えています。体力が足りません。

あとは，にゃんこ先生の解説サイトをたくさん見て，本番のシミュレーションをしていました。

www.path-to-success.net

問題集の回し方とか

問題集をn周する，の定義が人によって違うと思うので，私の中の定義をここに書いておきます。
私は，初見で自力で解けた問題は基本放置してます。できる問題にばっかり時間を割いても無駄なので。解けなかった問題に付箋を貼り，3日後くらいに付箋が張られている問題をリベンジして，解けたら付箋を折って，1か月後くらいにまた付箋を戻して……を繰り返していました。付箋がある問題を解きなおすのが私にとっての1周です。最後の方とか3問くらいしかありませんでした…()
とにかく，勉強の目的は知識をつけて苦手をつぶすことです。問題集を解くことが目的になったらだめです。となると，一度自力で解けた問題はしばらく放置して，苦手な問題にいっぱい時間を使う方がいいのかなぁと思います。時間はかかりますけどね。早めに始めたらいい話です。

また，有機化学のところで暗記シートの話をしましたが，このアプリをiPadで使っていました。

‎「イルカの暗記シート」をApp Storeで

ちょっと重たいところもあるけど，ノートで書いたものをPDF化して，それをインポートしたらルーズリーフに赤シートかぶせているのと同じになり便利です。赤シートも簡単にずらせるし。

おわりに

編入試対策の本は漫画とかラノベと比べるとめっちゃ値が張りますが，ケチらないほうがいいと思います。自分への投資です。(私は挙げた本を全部バイト代で買いました)iPadとかも買えるなら買ったほうがいいと思います。勉強中に手が真っ黒になるのすごくストレスなので。特に私は左利きなので，横書きでめちゃくちゃ手も袖も黒くなってました。

記事は以上です。
何か気になることがあったらTwitter(@fukuro_hoho)までDMしていただけると，私が自分のペースで返します。
では。

大学編入体験記(vs専攻科/阪大/京大)

久しぶりのブログだ……。ふくほです。
高専の5年生になり，大学編入試験を受けたので，そのことについて書きます。
使った参考書と科目別の具体的な勉強法は，別の記事にまとめています。もしよかったらそれも見てください。↓

後で書きたいことができたら最後に「追記n」として続けていきます。
すごく長い記事になるので，適当に読んでね。

受験校と志望動機

受験校は以下です。

第一志望は京都大学です。昔ELCASを受講したときは楽しかったし，京都に通いたいと思ったからです。
ずっと大学編入を意識していて，東大か京大に行けたらいいな～と思っていたところ，東大は教養科目の履修が京大と比べてキツそうだとTLを見てなんとなく思ったのと，関東はこてこての関西人である私の肌に合わないと感じたので，東大志望をやめました。記念受験しようかなと思ったのですが，東大受験にかかわる費用は全額小遣い負担になったのと，調査書などの申請が面倒だったのでやめました。
専攻科は実質進級するだけなので心身の負担が少ないし，学費も大学と比べると安いので受けました。
大阪大学は，関西圏では特にレベルの高い大学だし(関西から出たくない)，面白そうな学科があったので受けました。

受験結果は，すべて合格でした。ほっ。

受験前の過ごし方とか

上述の通り，大学編入自体は高専に入ったころから意識していました。
私は中学生のころから体調を崩しやすく(詳細は割愛)，高校に進学して大学受験するという選択肢で勝ち進んでいけるのか不安だったので，試験まで時間があってかつ科目が少ない編入試を選んだという側面もあります。(当時本当にここまで意識してたかは，忘れた)あと私の年から共通テスト導入だったので，逃げたかった。
実際，高専の1,2年では体調が悪くて学校に出られない日が多かったので，高校に行ってたらまともに進学できてなかったんじゃないかと思います。2年生の時は休み過ぎてちょっと留年しそうになりました。3年になると，そろそろ慣れてきたのと，春にコロナ1波がやってきたので，家にいる時間が増え体調が悪い日が減ってきました。なので，大学編入試の勉強は3年生の春からゆっくり始めました。

3年

数学ばっかりやってました。
とりあえず微積と線形代数の予習をして，編入向けの問題集をオンライン授業中の空いてる時間にゆっくり解いてました。オンライン授業最高。後期は応用数学の予習を数学の授業中とかにやってました。本質を全然理解してないまま，とりあえず問題集を解いていた感じでした。
微積の予習は，アウトプットとしてブログに書いたりもしていました。微分方程式の解法とかね。(過去のブログとか探すと見れます)
TOEIC 公開テストを申し込みましたが，コロナで流れました。(そもそもなんで申し込んだんだっけ……。)

4年

春にTOEIC IPを受けました。鉄壁で単語の確認した以外はノー勉でした。625点でした。
また，冬には学年でTOEIC IPを集団受験しました。このときも鉄壁以外何も使ってません。675点でした。私はもっと英語を頑張れ……。

6月くらいにiPadとApple Pencilを買いました。高かったですが，通学電車でも勉強ができるようになって最高です。電車でレポートに使う図を描いたりもできます。
初等力学と電磁気は，ちょっと授業の先取りをしながら，問題集を解いてました。
応用数学の試験の平均点が低くてちょっと頑張って勉強したので，応用数学が得意になりました。
4年生になってからもオンライン授業になったことがあったので，3年の時に解いていた数学の問題集を解きなおしていました。

この頃は出願資格はありませんが，京大の出願書類を請求してみました(テレメールなのでらくらく)。調査書のフォーマットを見て震えました。





5年になる前の春休み

そろそろ本格的に受験勉強をしようと思い，バイトをしばらく休ませてもらうことにしました。無収入生活の始まりです。

化学の対策を始めました。ずっと化学は苦手だし好きになれなくて後回しにしていたので，他の科目と比べると手を付けるのが遅かったです。有機化学と理論化学の本を買ってちょっと勉強しました。数学の問題集も一冊増やして解いてました。


vs TOEFL

3月末に，京都大学に提出する用のTOEFL iBT を受験しました。受験料が円安も相まってすごく高かったです。なんか今の円安は当時と比べ物にならないようなことになってるけど……。過去編入にTOEFLを使った先輩方は3回くらいTOEFLを受けてますが，私はそんなにお金を書けたくなかったので頑張って1回でせめて60は超えたいな～と思っていました。
3週間くらいで4技能全てを勉強したので疲れました。ここ数年鉄壁以外ほとんど読んでいなかったので英語の勉強方法がわからなくなったし，長文を読むと頭が痛くなったので，ずっと後回しにしていたらいつの間にか試験日が近づいていました。とりあえず鉄壁と，TOEFL用の単語帳(3000単語くらい)に載っていた単語をQuizletで詰め込みました。(短期間で一気に覚えるのは苦手じゃない)他にもちょっとだけ演習をしました。
Speakingにめっちゃ苦労しました。普段英語を喋ったりしないし，時間制限が厳しいし……(軽度な吃音を持っているので，45秒で喋り切るのが無理でした)

当日は大阪の中津に受験に行ったのですが，外は雨だし，迷子になるしで大変でした。拘束時間も4時間くらいですごく疲れました。チョコレートなどの糖分を休憩中に摂取することができるので必ず持って行くようにしましょう。カフェインも必要だと言っている人もいますが，利尿作用があるので摂りすぎは良くないと思います。(試験中にトイレに行くのは厳しいので)私はダースチョコとポカリスエットを朝コンビニで買って，休憩中に飲んでました。
TOEFL後，15時に食べたお昼のステーキが最高でした。

スコアは……

やっぱりSpeakingが一番ダメでした。Listeningは知ってる化学の話が出たので，英語はあんまり聞き取れなかったけど持ってる知識で問題を解いたらなんかWritingよりも点数が高くてびっくりしました。英作文は頑張ったのになぁ。



5年 4~6月

学校が始まってしまいました。授業と通学で体力的に大変でしたが，周りも進学モードだったので捗りました。
周りの人と専攻科の過去問の答え合わせをしながら，専攻科に出る専門科目(電気回路，電磁気)の復習をしていました。
気が向いたら他の科目の演習もしてました。
5月に20歳になったので，週末の夜たまにお酒を飲んだりしてリラックスしていました。

またこの頃，受験校の出願及びその準備が大変すぎて毎日泣きそうになってました。郵便制度も普段使わないので頭を抱えました。(まじで年賀状くらいしか送らないので)20歳，はじめてひとりで切手を買う……。
私はこれにかなり気力を吸われたので，大学を7個とか受けてる人は本当にすごいなと思いました。


vs 専攻科(6/18)

6月の真ん中に，専攻科入試がありました。コロナ対策で，当日の朝は体調チェックシートを提出するのですが，記入するの忘れててめっちゃ焦りました。幸いにも会場に持って行ってたので，その場で書いて出しました。
試験科目は数学と専門科目(電磁気，電気回路)でした。

数学は答えのみ記入するスタイルです。途中で計算ミスがあれば地獄を見ますが，記述に気を遣わなくていいので楽でした。基礎的な問題が多かったです。1問目に出てきた分数関数，2週間くらい前に受けた数学特講の試験と全く同じで面白かったです。極値とグラフの概形を覚えていたのではじめなにも計算せずに記憶で答案用紙を埋めました。わろた。
試験時間は90分だったのですが，50分で全部解ききったので暇でした。余った時間はもう一度計算をしたり(特にヘシアンとか間違えやすいので)，シャーペンをくるくる回したり，時計を眺めたりしてました。

専門科目は爆死しました。電磁誘導の向きを間違えたり，コンデンサに定常電流を流してしまったりしました(なんで？)。
今年は，今までになかった磁気回路問題が出ました。回路は作れたのですが，なんか途中経過をどう書いていいかわからなかったので答えだけぼんぼん書きました。点数入ったのかな。後から考えると，根本からいろいろ間違っていることに気づいたので，多分半分くらいしか取れてません。欠点です。

合格発表の日は緊張のせいかおなかが痛くてしばらくトイレにこもっていました。まあ，合格できてよかったです。



5年 7月前半

専攻科の合格発表まではやる気が出ず，ぼーっとしていました。発表後は，7月の真ん中に阪大の入試があったため，急いで阪大の過去問を5年分くらい解きました。この頃まで，阪大基礎工は毎年力学で剛体を出しているということは知りませんでした。物理は力学，電磁気学，熱力学から2問選択なのですが，基本熱力学は捨てるスタイルで勉強しました。カルノーサイクルと気体分子運動論の問題だけ解けるようにしておきました。(勉強できる文献が多かったのと過去問を見るとよく出てたので)専門科目は2年分解いてあとは眺めただけでした。
英語は相変わらず鉄壁と過去問以外何もしませんでした。中学生の時と高専1年生の時しかまともに英文法の勉強をしていないので，英語の勉強方法を忘れました。



vs 阪大(7/9,10)

試験中にずっとセミが鳴いててうるさかったです。会場には時計がないのですが，時計を持って行くのを忘れて詰みました。体調チェックシートは(専攻科でどきっとしたので)忘れずに書いてから持って行ったのに。時間配分は感覚と腹時計で何とかしました。試験科目は英語，数学，物理，専門科目(応用数学)でした。

まずは英語でした。英訳は宇宙空間に進出しまくってるドローンのことと、人工知能の透明性っぽいことについてでした。高専向けだなあと思いました。それっぽい日本語を書きました。
長文は、(あの Wordle の)New York Timesの引用でした。動物を使って人間の習慣を実験するという(?)話でした。こういったトピックはほとんど読まないので楽しかったです。(解けたとは言ってない)
英作は、PCの内蔵マイクでリモート会議とかしてると音質落ちるよねみたいな話があり，コロナ禍ならではだと感じました。とりあえず書ききりました。

次は数学でした。1問目の微積では、全微分、接線、接平面を求める基礎的な問題がまずありました。その後，接平面が必ず通る点を求める問題がありました。はじめは怯みましたが，解けました。阪大の特徴なのか，最後の問題以外は典型問題な気がします。
2問目の線形代数は、線型写像が出ました。いい感じに誘導がかかっていて解きやすかったです。ほとんど計算するだけだったので，ここは10割取れたと思いたいです。
3問目は確率分布に関する問題でした。誘導がかかっていたのですが，最後のエントロピー(熱力学のやつじゃなくて，情報理論で出てくるアレ)を最大化するような確率分布を求める問題がいまいちよくわかりませんでした。とりあえず誘導がかかっていたので二項分布だと仮定して係数を計算しました。明らかに記述不十分です。後から調べたら，条件が2つある時の1変数関数の条件付き極値に帰着させたらよかったみたいです。面接が終わった後にわかって虚無になりました。

その次は物理でした。力学は例年通り剛体が動いてました。今年は剛体振子。序盤は典型問題でしたが，最後はあまり自信がないです。
電磁気は、まさかのローレンツ力によって回転する電荷の問題でした。去年受けた学校の試験問題にそっくりだったのでラッキーでした。電荷、くるくる〜。二階微分方程式を解く過程がめんどくさく，とても長いと感じたので，ラプラス変換を使って解きました。振動とか回転の運動方程式はラプラス変換を使うと解きやすいのでおすすめです。(口頭試問とかで聞かれるかもしれないので理論も理解しておくと尚良い)
熱力学は図だけ見て，何もわからなかったので，問題文も読まずにそっと閉じました。

最後の応用数学は，2問から1問(小問5個くらい)選択でした。小問の1~3は、ちょっと面倒な微分方程式を解く問題でした。ロンスキアンとか畳み込みを使ってごり押したら解けました。求まった解を微分方程式に代入したところ合ってたので，間違ってないと思います。4,5はフーリエ級数展開をして、そこから非自明な級数を求める問題でした。書く量が多すぎて、解答用紙が足りませんでした。奇関数だったのでなるべく計算量を減らしていく方針で頑張りました。合ってるか不安です。

試験後には机の上が消しゴムのカスだらけになっていました。普段iPad & Apple Pencilでundoばっかり使っているので，消しゴムで大量にこするとすごく疲れました。消しゴムのカスを回収してくれた人と友達になりました。本当にありがとう。

翌日には，面接がありました。名目上は口頭試問ですが，数理科学コースは前日にペーパーテストがあったのでそれについて少し突っ込まれる程度でした。時間は全員15分くらいだったみたいです。聞かれたことはうろ覚えですが，こんな感じでした。

  • 志望動機
  • 試験の出来はどうだった？

→まずまずですかね。(ここ，私はこう言っちゃったんですが，試験でミスしたところを挽回するチャンスだったらしいので自己採点をちゃんと言った方がよさそうです)

  • 英語は得意か？

→苦手意識はないけど得意かといわれると怪しいです。(試験結果見てるはずなのになんで聞かれたん？)

  • 英語論文を読んだりしないのか？

→最初は自力で頑張るけど，機械翻訳使っちゃいます(笑われた)

  • 数理科学の分野の中では，特に何に興味がある？

→全部ですが，特に微分方程式です

→解をプロットすると綺麗なので好きです

→昔習ったけど忘れました(爆死。半年前にやったけど微塵も復習していなかったので散りました)

  • 今まで参加した外部のもの(情報科学の達人とかELCASとか)は，どのように数理科学と繋がっていた？

→(よく考えると外部のやつはあんまり数学数学してないので，あまり繋がってなくね？と感じてしまい，爆死)

他にもあったかもしれません。部屋に入ると，目の前に昨日の試験問題がありました。面接官の先生方は9人くらいで，全員何か書類を持っていました。(調査書とペーパーテストの結果かな？)9対1は初めてだったのですごく緊張しました。

あと，面接でめっちゃ英語のこと聞かれたんですが，そんなに英語の試験が悪かったんでしょうか。「英語論文は機械翻訳を使っちゃいます」，って話をすると笑われたので，あわてて「でも機械翻訳が誤訳をしてないかはある程度確認をしています！」というともっと笑われました。カバーになってなかったです。機械翻訳の誤訳確認をちょっとしているのは本当です。

怖かった気持ちはありましたが，あの阪大で試験を受けられるというのはとても貴重な経験で，楽しかったです。受験会場で友達もできたのでよかったです。(その子も受かったのでとても嬉しい)


合格発表の時間は授業中で，自分の番号があることを確認した後は手の震えが凄かったです。


5年 7月後半 ~ 8月

例のごとく，阪大合格発表までぼーっとしてました。発表後も，合格してると思ってなかったのでびっくりしてしばらく勉強が手につきませんでした(言い訳)。合格報告で一番びっくりしてたのは母でした。

さて，新型コロナの感染がまた拡大してる中，定期試験を何とか終えて夏休みに突入しました。阪大から合格をもらっているのもあってか，あまりやる気が全然出ずぼーっとアニメを見たりしていました。周りもほとんど進路が決まり，置いていかれた感じがすごかったです。ちょこちょこ復習したり，京大の過去問を解いたりしていました。この頃アニメ合計6クールくらい一気見したなんて言えない……。

vs 京大(8/30,31)

ラスト受験は本命の京都大学でした。京都で一人暮らしをしている仲のいい友人の家に泊めてもらい，そこから大学に向かいました。
今年の工学部受験生は全体で15人（出願したのは18人で，3人辞退(体調不良？)）でした。緊張で試験の序盤は胸焼けがすごかったですが，数学の試験に集中してたらいつの間にか消えてました。
初日の試験科目は数学，物理・化学でした。

まず数学。120分で大問は4つでした。微積分が2問，線形代数が2問，確率が1問でした。線形代数は，3次正方行列の固有値を求めたり対角化するだけの一見簡単な問題ですが，真ん中に文字が含まれていたのですごく計算ミスを煽られました(引っかかったかも)。微積は，ほとんどやるだけの問題でしたが，一問だけ留数定理を利用する広義積分(因数分解でごり押したら解けるけど大変)があり，方針は書いたものの解答を書ききれませんでした。
確率は，感染症に関する問題でした。偽陽性とか偽陰性とかの話が出てきて面白かったです。ベン図さえ描ければ難しくない問題でした。

次に，物理・化学。物理と化学を合わせて120分でした。物理と化学それぞれに問題冊子と回答冊子があるので，机の上に4冊も冊子があり管理が大変でした。
物理は，平面で楕円軌道を描いている質点についての考察でした。基礎的です。電磁気は，今まで見たことのない穴埋め問題でした。電磁誘導と定常状態のRLC回路の融合問題でした。運動方程式が立てられたら問題ありません。(多分)最後の，インダクタのエネルギと運動エネルギと位置エネルギを x-Uグラフに示す問題がありました。割と電磁気に関してはかなり場数を踏んだつもりでしたが，見たことない問題で計算するのが楽しかったです。(計算したら，位置エネルギは直線，運動エネルギは放物線，インダクタのエネルギは位置エネルギと運動エネルギの差になりました，合ってるか知らんけど。)

化学は，熱力学，無機，有機の3問構成でした。熱力学はよくわかりませんでした。(断熱過程の仕事とか知らなかった)無機は，SrTiO の単位格子に関する問題でした。配位数と，結合距離を求めるだけだったので簡単でした。有機は，グルコースの還元性以外はだいたい分かったような気がします。(グリニャール試薬の問題がちょっと怪しいかも)化学に関しては，3割あれば万々歳だと思っていたのですが，半分は取れた気がします。(本当に？)


試験終了後に，消しゴムのカスをどこに捨てたらいいかわからずおどおどしていたら，同じくおどおどしていた子と友達になれました。すごく嬉しいです。


翌日は口頭試問でした。口頭試問とはいえ，ほぼ普通の面接でした。聞かれたことを書いておきます。

  • 学部卒業後の進路はどう考えている？

→博士課程に行けたら行きたいけど，経済面などで厳しかったら修士卒で就職して企業で研究開発したい(できるのかな)

  • 数理工学コースの志望動機は？

→2年くらい前に編入した先輩から履修要覧を見せてもらい，計算機と数理の履修を強く推奨する科目の中でよりおもしろそうだと思ったのが数理だったからです

  • 卒業研究は何をしてる？

→秘密(面接ではちゃんと研究背景から利用手法まで答えました)

  • 去年高専祭で作ったものについて説明して

→CNNで犬と猫を学習させて，そのモデルに人間の顔を突っ込んで，モデルがどう判定するのかを楽しむっていうおもちゃを作りました

  • CNNってすごく便利なんだね

→確かに便利だし，転移学習などを用いると精度が上がることもあるけれど，そうすると中が完全にブラックボックスになってしまうので怖さもあります。もっとCNNの中を勉強していかないといけないと思います

  • ELCASでどんなことしたの？

→ラグランジュの運動方程式を三項間漸化式に近似して倒立振子を制御する，ということと，ソリトンセルオートマトンをPythonで実装して交通渋滞のシミュレーションを行うということをしました

  • 情報科学の達人って何？どうやって選ばれたの？

→NII主催のGSCで……(ここで詳細は割愛，気になる人はググってください)選考は過去の実績などの作文でした

→一応最後まで答えはしたけど計算合ってるかわからないです……

→今回の編入試で出た範囲は主に3年生で習った内容ですが，この頃オンライン授業だったのもあり，ほとんど独学してわからないことはTwitterの大学生に聞いていました

  • 学校の先生には質問しようと思わなかったの？

→Twitterで大学生に聞く方が気軽なので…

  • 独学ではどんな参考書を使ってたの？

→マセマのことを話すとちゃんとした専門書の方がいいよ～，余談ですがと言われた


他にもあった気がしますが，印象に残ったのはこんな感じです。あまり難しいことは聞かれませんでした。ずっと和やかな雰囲気でした。形式的なこと(前半)を聞かれてからCNNとかELCASとかの話になったのですが，面接後半ですごく話が盛り上がってみんなで笑ったりもしていました。なるべく聞かれたことにだけ答えるのではなく，そこから先生たちが興味のありそうな内容に話を膨らませるように意識していました。(～の授業あるの？って聞かれて，ありますとだけ答えても味気ないので，ちょっと補足するとか)
それに，試験結果はほとんど筆記で決まると聞いていたので，多少変なことを言っても大丈夫だろうと気楽な気持ちでいました。実際それがちょっとした笑いになったので悪くなかったです。



合格発表の日は合否に関わらず精神状態が正常ではなかったので，カラオケに行き，カラオケの中で合格発表を見ました。ヒトカラ料取られました……。自分の番号あった……。





最後に

編入試験対策は早めにした方がいいです……。試験が近づいてくると，「今詰め込んでも試験本番で出るかなんてわからないし…」ってモチベが下がります(私の場合)。直前じゃなくてもモチベが下がる時がよくあります。そんな時は，罪悪感を覚えるくらいだらけましょう。1日でアニメ1クール以上見るとか…。精一杯だらけると，さすがに勉強しないとまずいな？って思えるはずです。

また，編入界隈で言われがちなことを言うと，勉強時間が長いほど成果が出るというわけでは決してないです。期間は長い方がいいと思うけど。よく，1日何時間勉強してるの？って聞かれるのですが，時間は計ってません。(やる気があった日のiPadのスクリーンタイムは普通に10時間を超えるし，やる気のない日は10分やったかすら怪しい)(昔Study Plusをやっていたのですが，時間で満足したらダメな気がしてやめた)
やる気が出たときにどれだけ知識を吸収して，またそれを外に出すかが重要だと私は思っています。嫌々やっても何も頭に残りません。実際，私は中学の時に保健体育でやった柔道のルールとかもはや何も覚えてません。ずっとやる気が出ないのなら勉強なんて必要最低限以外はしなくてもいいとさえ思います。

あとはなんだろう……。試験，意外と楽しいです。遠足気分で，気楽にいきましょう。試験会場で他高専の人と知り合いになれると嬉しいし，あんまり周りを敵だ敵だと思いすぎることはない気がします。少なくとも京大と阪大の編入試は定員制じゃなくてボーダー制って聞きました。今まで解いた問題集のどんな問題とも(パターンは同じでも数字は違うはず)違った問題を，高専よりも大きい大学で解ける！映画の公開日にるんるんで観に行くようなもんです。

最後に，大事な試験の前はく寝ましょう。夜の9時に布団に入るのが目標くらいで。当日の体調はかなり大事です。

ということで，このブログはそろそろ終わりにします。冗長ですみません。
何か気になることがあれば，Twitter(@fukuro_hoho)にDMしてくれると，(私のペースなので遅いかもしれませんが)お答えしようと思います。
では。

正弦波っぽい放物線をフーリエ級数展開して遊んだ話

ふくほです。
またまた久しぶりの記事になってしまった。

今回は，放物線をふたつ組み合わせた，めっちゃ正弦波っぽいグラフをフーリエ級数展開したらどうなるかを考えてみました。

きっかけ

高専1年生で初めて正弦波を見たとき，放物線の合成にしか見えませんでした。
ただ，話によると正弦波と放物線は全く別物。まじ？
そのだいぶ後に単位円の話を聞いて，放物線と無関係であることは納得したのですが，やはり形が似ているような……。

ここで，割と最近知ったフーリエ級数の話。周期関数を三角関数の和の形で表すというものです。
放物線をフーリエ級数展開すると面白いことになりそう！
ということで，やってみました。

今回は遊んだだけなので，手計算はせずにwolframとpythonに頼りきって演算をしました。

準備する放物線

y =\sin{x}に似た放物線として，以下のような放物線を用意しました。
Parabola1 : y = -\dfrac{4}{\pi^2}(x-\dfrac{\pi}{2})^{2} + 1\\ Parabola2 : y = \dfrac{4}{\pi^2}(x-\dfrac{3\pi}{2})^{2} - 1
グラフにするとこんな感じ↓
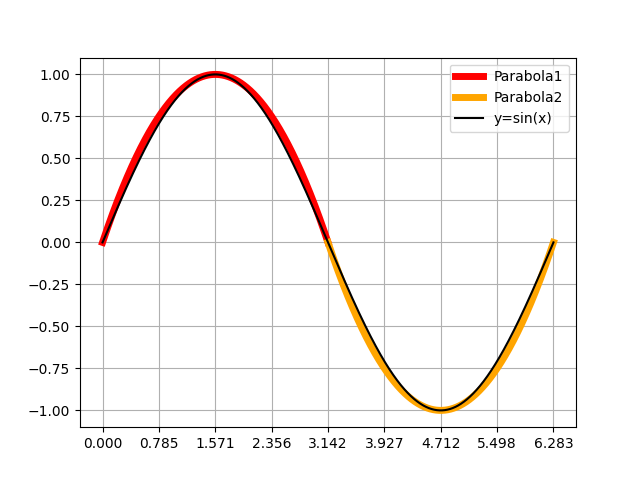
f:id:fukuro_hoho:20211204133752p:plain
正弦波と重ねてみても似ていることがわかります。
まあ，ちょっと放物線の方が広がってる感じするけど……。

放物線は，頂点の座標とx軸との交点の座標から決めました。

フーリエ級数展開してみる

それでは，前の放物線の組み合わせを周期 2\piの周期関数としてフーリエ級数展開してみます。
y \sim c_{0} + \sum_{n=1}^{\infty}(a_{n}\cos{nx}+b_{n}\sin{nx})
フーリエ級数展開については記事を書いたことがあるので，貼っておきます。
fukuro-hoho.hatenablog.com

今回は1周期の積分値が0になるのはグラフから明らかなので， c_0=0となります。
また，この関数は奇関数となるため， a_n = 0が任意の1以上のnについて言えます。

さて，残りの b_nですが，これは手計算は面倒なのでwolfram alphaに投げました……。
計算結果はこんな感じ。
b_n = \dfrac{16}{(n\pi)^3} (1 - (-1)^{n})

nが偶数の時 b_nは0となり，奇数以外の時はb_n = \dfrac{32}{(n\pi)^3}になるみたいです。

www.wolframalpha.com

求まったb_nを， n=1から順にグラフにしてみると，こうなりました。
f:id:fukuro_hoho:20211204141028p:plain
え……すご。 n=1ではほぼ1になっていますが，それ以外での値はほぼ0になっています。
主成分以外の周波数成分はほとんど含まれてないんですね。
ちなみに，数値を出力させるとこんな感じ。
f:id:fukuro_hoho:20211204141645p:plain
n =1の時しかほぼ値がないといった感じ。
この値は，前の式から n^{3}に反比例するので，かなりの速さで0に収束していきます。

うわ～～，すごい……。
これだと，放物線と正弦波を初見で同じだと感じるのも仕方がなさそうです。(多分)
本当に感動して一晩寝るのに苦労しました。

思い切ってソースコードを公開しちゃう

今回は手計算なしで，すべてpythonとwolframに投げたという話をしました。
ありふれたことしか書いていませんが，pythonのコードをせっかくなので公開しておきます。

まず，1枚目のグラフを描いてくれたプログラムから。

import math
from matplotlib import pyplot as plt
import numpy as np

# 横着者なので
pi = math.pi
def sin(x):
    return np.sin(x)

x1 = np.linspace(0,pi,10000)
x2 = np.linspace(pi,2*pi,10000)
x = np.linspace(0,2*pi,20000)

y1 = -4 / (pi*pi) * (x1 - pi/2)*(x1 - pi/2) + 1
y2 = 4 / (pi*pi) * (x2 - 3*pi/2)*(x2 - 3*pi/2) - 1

plt.plot(x1,y1,lw = 5,color = 'red',label = 'Parabola1')
plt.plot(x2,y2,lw = 5,color = 'orange',label = 'Parabola2')
plt.plot(x,sin(x),color = 'black',label = 'y=sin(x)')
plt.xticks(np.linspace(0,2*pi,9))
plt.grid()
plt.show()

次に，各 nに対してフーリエ係数を求め，グラフを出力してくれるプログラム。

import math
from matplotlib import pyplot as plt
import numpy as np

# 横着者なので
pi = math.pi
def pow(x,n):
    ans = 1
    for i in range(n):
        ans *= x
    return ans
def cos(x):
    return np.cos(x)

n = np.linspace(1,21,11)
b = (16 / pow(n*pi,3)) * (1 - 1 * cos(n*pi))

cnt = 1
for i in b:
    # 出力をそろえる
    if cnt < 10:
        print('n :', cnt, '   b_n :', i)
    else:
        print('n :', cnt, '  b_n :', i)
    cnt += 2

plt.xticks(np.arange(1,22,2))
plt.plot(n,b,color = 'red')
plt.grid()
plt.show()

最後に

長年のモヤモヤがすっきりしてうれしいです。
ただ，記事を書くことを試験期間中に思い立ってしまったことだけが反省点。今回の試験範囲にフーリエ級数展開の話があったし，これで試験勉強したってことにならないかなぁ……。(多分ならない)

3次方程式を解きたすぎてカルダノの公式を導出してしまった話

ふくほです．
今回は3次方程式の解の公式の1つであるカルダノの公式ついてまとめてみました．

1. 3次方程式の解の公式：カルダノの公式

カルダノの公式と呼ばれている3次方程式の解の公式があります．
3次方程式(今回はx^3の係数を1としています)
\begin{eqnarray} x^3 + a x^2 + b x +c = 0 \tag{1} \end{eqnarray}
の3つの解をx_1, x_2, x_3とおいたとき
\begin{eqnarray} \begin{split} x_1 &= \sqrt[3]{ -\dfrac{27c+2a^3-9ab}{54} + \sqrt{\left( \dfrac{27c+2a^3-9ab}{54} \right)^2 +\left( \dfrac{3b-a^2}{9} \right)^3 }} \\ &\quad+ \sqrt[3]{ -\dfrac{27c+2a^3-9ab}{54} - \sqrt{\left( \dfrac{27c+2a^3-9ab}{54} \right)^2 +\left( \dfrac{3b-a^2}{9} \right)^3 }} -\dfrac{a}{3}\\ x_2 &= \omega \sqrt[3]{ -\dfrac{27c+2a^3-9ab}{54} + \sqrt{\left( \dfrac{27c+2a^3-9ab}{54} \right)^2 +\left( \dfrac{3b-a^2}{9} \right)^3 }} \\ &\quad+ \omega^2 \sqrt[3]{ -\dfrac{27c+2a^3-9ab}{54} - \sqrt{\left( \dfrac{27c+2a^3-9ab}{54} \right)^2 +\left( \dfrac{3b-a^2}{9} \right)^3 }} -\dfrac{a}{3}\\ x_3 &= \omega^2 \sqrt[3]{ -\dfrac{27c+2a^3-9ab}{54} + \sqrt{\left( \dfrac{27c+2a^3-9ab}{54} \right)^2 +\left( \dfrac{3b-a^2}{9} \right)^3 }} \\ &\quad+ \omega \sqrt[3]{ -\dfrac{27c+2a^3-9ab}{54} - \sqrt{\left( \dfrac{27c+2a^3-9ab}{54} \right)^2 +\left( \dfrac{3b-a^2}{9} \right)^3 }} -\dfrac{a}{3} \end{split} \tag{2} \end{eqnarray}
となるという公式です．(ミスタイプしてる気しかしない)ただし，\omegaは1の3乗根, \dfrac{-1\pm \sqrt{3}i}{2}のどちらかであるとします．\left(\dfrac{-1 + \sqrt{3}i}{2}\right)^2 = \dfrac{-1 - \sqrt{3}i}{2}, \left(\dfrac{-1 - \sqrt{3}i}{2}\right)^2 = \dfrac{-1 + \sqrt{3}i}{2}なので，\omegaはどっちをとってもいいです．
ぱっと見うげっとしませんか？私はします．洗面所にずっと貼ってたんですけど，覚えることはできませんでした()
カルダノの公式という名は，16世紀半ばにジェロラモ・カルダーノが「偉大なる術」という著書にこの公式を載せたことが由来だそうです．
当時のイタリアには3次方程式の数学試合があり，解の公式はホットなネタだったみたいですね．カルダーノはタルタリアという別の人物からもらった公式を自分の著書に載せてしまったらしく，タルタリアとカルダーノの間に争いが生じたんだとか．大変ですね．一部の人々からは，カルダノ・タルタリアの公式とも呼ばれているみたいです．
タルタリアとカルダーノの情報はWikipediaにたくさんありました，面白いのでぜひ読んでみてください．
ja.wikipedia.org
ja.wikipedia.org

はじめはこの公式を丸暗記しようと思ったのですが，さすがに無理だと思ったので導出過程を追っていき自力で導けるようにしたいと思います．がんばるぞ～．

2.カルダノの公式を導いてみる

2.1.立方完成をする

まず，(1)式を立法完成してx^2の項を何とかします．
\begin{equation} \left(\alpha + \beta\right)^3 = \alpha^3 + 3\alpha^2\beta + 3\alpha\beta^2 + \beta^3 \end{equation}
を思い出して，これの逆をやります．よ～し．
\begin{eqnarray} x^3 + a x^2 + b x +c &= \left(x+ \dfrac{a}{3}\right)^3 - 3\left(\dfrac{a}{3}\right)^2 x - \left(\dfrac{a}{3}\right)^3 +b x + c \\ &= \left(x+ \dfrac{a}{3}\right)^3 + \left(-\dfrac{a^2}{3} + b\right)x +c - \dfrac{a^3}{27} = 0 \tag{3} \end{eqnarray}
これでとりあえずx^2の項は何とかなりました．さて，次．

2.2.変数を増やしてみる

見出しの作成が下手．
次に x+ \dfrac{a}{3} = s + t\tag{4}と置換してみます．(本とかほかの記事だとu,vに置換しているものが多いのですが，手書きにすると見分けがつかなくて間違えることがあるので私は避けています．勝手なルールです，ごめんなさい)
さて，(3)式に(4)を代入して整理してみましょう．
\begin{eqnarray} \left(x+ \dfrac{a}{3}\right)^3 + \left(-\dfrac{a^2}{3} + b\right)x + c - \dfrac{a^3}{27} &=&\left( s + t \right)^3 + \left(-\dfrac{a^2}{3} + b\right)\left(s + t - \dfrac{a}{3} \right) + c - \dfrac{a^3}{27} \\ &=&s^3 + t^3 + \left(3st - \dfrac{a^2}{3} + b\right)\left( s + t \right) - \dfrac{a}{3}\left(-\dfrac{a^2}{3} + b\right) + c - \dfrac{a^3}{27} \\ &=&s^3 + t^3 + \left(3st - \dfrac{a^2}{3} + b\right)\left( s + t \right) - \dfrac{ab}{3} + c + \dfrac{2a^3}{27} \\ &=&s^3 + t^3 + \dfrac{9st-a^2+3b}{3}\left( s + t \right) + \dfrac{-9ab+27c+2a^3}{27} = 0 \tag{5} \end{eqnarray}
ここまでの整理，合ってるはず？です！

2.3.2変数を用いて２次方程式に持っていく

次に，(5)式を満たす\left(s,t\right)の組として，以下の2つの条件をを満たすものを考えます．
\begin{eqnarray} s^3+t^3 + \dfrac{-9ab+27c+2a^3}{27} &=& 0 \\ s^3+t^3 &=& - \dfrac{-9ab+27c+2a^3}{27}\tag{6} \end{eqnarray}
\begin{eqnarray} 9st-a^2+3b &=& 0\\ s t &=& -\dfrac{-a^2+3b}{9} \\ s^3 t^3 &=& -\left(\dfrac{-a^2+3b}{9}\right)^3\tag{7} \end{eqnarray}
(7)式において，なぜ両辺を3乗したのかはおわかりでしょうか…，これは２次方程式の解と係数の関係(KKKとか言って遊ばれるやつ)を利用するためです．
つまり，s^3, t^3は，\lambdaについての２次方程式
\lambda^2 + \dfrac{-9ab+27c+2a^3}{27}\lambda -\left(\dfrac{-a^2+3b}{9}\right)^3 = 0 \tag{8}
の2つの解に他ならないのです．すごい！
実際に(9)を解いてみましょう．２次方程式の解の公式は中学数学レベルなので既知として求めると，
\begin{eqnarray} \lambda &=& \dfrac{-\dfrac{-9ab+27c+2a^3}{27} \pm \sqrt{\left(\dfrac{-9ab+27c+2a^3}{27}\right)^2+4\left(\dfrac{-a^2+3b}{9}\right)^3 } }{2}\\ &=& -\dfrac{-9ab+27c+2a^3}{27\cdot 2} \pm \sqrt{\left(\dfrac{-9ab+27c+2a^3}{27}\right)^2\cdot \dfrac{1}{4}+4\left(\dfrac{-a^2+3b}{9}\right)^3\cdot \dfrac{1}{4}}\\ &=& -\dfrac{-9ab+27c+2a^3}{27\cdot 2} \pm \sqrt{\left(\dfrac{-9ab+27c+2a^3}{54}\right)^2+\left(\dfrac{-a^2+3b}{9}\right)^3} \tag{10} \end{eqnarray}

2.4.ここからは頑張るしかない

ここで\pmの+をs, -をtとしても一般性は失われないため，
\begin{eqnarray} s^3 &=& -\dfrac{-9ab+27c+2a^3}{54} + \sqrt{\left(\dfrac{-9ab+27c+2a^3}{54}\right)^2+\left(\dfrac{-a^2+3b}{9}\right)^3}\\ t^3 &=& -\dfrac{-9ab+27c+2a^3}{54} - \sqrt{\left(\dfrac{-9ab+27c+2a^3}{54}\right)^2+\left(\dfrac{-a^2+3b}{9}\right)^3} \end{eqnarray}
とすることができます．ここまで来たらもう少し！
また，
\begin{eqnarray} s^3 &=& -\dfrac{-9ab+27c+2a^3}{54} + \sqrt{\left(\dfrac{-9ab+27c+2a^3}{54}\right)^2+\left(\dfrac{-a^2+3b}{9}\right)^3}\times 1\\ t^3 &=& -\dfrac{-9ab+27c+2a^3}{54} - \sqrt{\left(\dfrac{-9ab+27c+2a^3}{54}\right)^2+\left(\dfrac{-a^2+3b}{9}\right)^3}\times 1 \end{eqnarray}
であるため，
\begin{eqnarray} s &= \sqrt[3]{-\dfrac{-9ab+27c+2a^3}{54} + \sqrt{\left(\dfrac{-9ab+27c+2a^3}{54}\right)^2+\left(\dfrac{-a^2+3b}{9}\right)^3} } \\ &\quad ,\omega \sqrt[3]{-\dfrac{-9ab+27c+2a^3}{54} + \sqrt{\left(\dfrac{-9ab+27c+2a^3}{54}\right)^2+\left(\dfrac{-a^2+3b}{9}\right)^3} } \\ &\quad ,\omega^2 \sqrt[3]{-\dfrac{-9ab+27c+2a^3}{54} + \sqrt{\left(\dfrac{-9ab+27c+2a^3}{54}\right)^2+\left(\dfrac{-a^2+3b}{9}\right)^3} } \end{eqnarray}
\begin{eqnarray} t &= \sqrt[3]{-\dfrac{-9ab+27c+2a^3}{54} - \sqrt{\left(\dfrac{-9ab+27c+2a^3}{54}\right)^2+\left(\dfrac{-a^2+3b}{9}\right)^3} } \\ &\quad ,\omega \sqrt[3]{-\dfrac{-9ab+27c+2a^3}{54} - \sqrt{\left(\dfrac{-9ab+27c+2a^3}{54}\right)^2+\left(\dfrac{-a^2+3b}{9}\right)^3} } \\ &\quad ,\omega^2 \sqrt[3]{-\dfrac{-9ab+27c+2a^3}{54} - \sqrt{\left(\dfrac{-9ab+27c+2a^3}{54}\right)^2+\left(\dfrac{-a^2+3b}{9}\right)^3} } \end{eqnarray}
を導くことができます．このままでは方程式の解を構成する\left(s,t\right)の組は3\times3で9個あるのでは？と思うかもしれませんが，(7)式の3乗する前の式より
s t = -\dfrac{-a^2+3b}{9}
を満たす必要があるため絞られます．この条件を満たす\left(s,t\right)は,
s'=\sqrt[3]{-\dfrac{-9ab+27c+2a^3}{54} + \sqrt{\left(\dfrac{-9ab+27c+2a^3}{54}\right)^2+\left(\dfrac{-a^2+3b}{9}\right)^3} }
t' =\sqrt[3]{-\dfrac{-9ab+27c+2a^3}{54} - \sqrt{\left(\dfrac{-9ab+27c+2a^3}{54}\right)^2+\left(\dfrac{-a^2+3b}{9}\right)^3} }
とすると，以下のようになります．
(s,t)=(s',t'),(\omega s', \omega^2 t'), (\omega^2 s', \omega t') \tag{12}
最後に，(4)式より x = s + t - \dfrac{a}{3}であるから，(12)の結果を代入してやります．これは(2)と一致します．
完成！

3. 感想とかまとめとか

3次方程式の解の公式は覚えておくとだいぶ便利だと思います．少なくとも私は全体的に数学の知識がなさ過ぎて，「これカルダノの公式覚えてたら計算はめんどくさいけど解けるだろうな…」みたいな問題に出会うことが割とよくあります．まぁ，3乗根の近似値を考えるのがしんどいんでしょうけど．
カルダノの公式のすごいところは，立方完成した後変数を増やしてしまうところにあるとよく言われているし私もそう思います．基本方程式を解くときは変数は減らす方向に進めるイメージなので…こんなところで解と係数の関係ってね．
全体の流れで行くと立方完成→変数を増やす→2次方程式の解と係数の関係を考える→頑張って計算って感じですか．これを覚えていたら多少時間はかかれども導ける気がします．すごーい．

最後になりましたが，もしも誤字脱字などの間違いがありましたらご一報ください，お願いします．
ということで，ふくほでした．ここまで読んでくださった方ありがとうございました！



参考文献

この記事を書くにあたって参考にしたリンクや書籍を貼ります．いつもありがとうございます．(既に貼っているものを除く)
1.LaTeXのsplitで数式モード内の長い数式を折り返す - Irohabook
2.はてなブログで記事中に数式を書く方法【TeXの簡単な使い方と支援サイト】 - sunsun fineな日々
3.三次方程式の解の公式 [物理のかぎしっぽ]
4.三次方程式の解の公式(タルタリア・カルダノの公式)

電気回路 / 三相交流入門してみた(2)三相電力, V結線について簡単に

ふくほです。
前回に続いて, 今回は三相交流での電力と, V結線について書いていこうと思います。
前回のやつはこれ。画像や電圧の定義などはそのまま使います。
fukuro-hoho.hatenablog.com

1 三相電力

電力の定義は, 電圧ベクトルと電流ベクトルの内積ですのでこれに忠実になると簡単に求めることができます。今回はΔ-Δ結線とY-Y結線のみ扱います。その他は適宜Δ-Y / Y-Δ変換をして対応することができるので。

1.1 Y結線での三相電力

Y結線での三相電力は以下の式で求まります。
\begin{eqnarray} W &=&\vec{I_a}\cdot\vec{V_a}+\vec{I_b}\cdot\vec{V_b}+\vec{I_b}\cdot\vec{V_b}\\ \end{eqnarray}
特にZ_a=Z_b=Z_cであるとき1つの負荷に流れる電流を\vec{I},1つの負荷での電圧降下を\vec{V}とすると
W=3\vec{I}\vec{W}=3IV\cos{\theta}
ここで\thetaは電流と電圧の位相差で, 負荷によって異なります。
また線電流が与えられているときは注意が必要です。線電流は相電流の\sqrt{3}倍になり位相が\dfrac{\pi}{6}[rad]ずれるため力率にも影響します。

1.2 Δ結線での三相電力

Δ結線での三相電力もY結線と同様に求めることができますが, 線間電圧を用いるときは注意が必要です。
線間電圧は相電圧の\sqrt{3}倍になり位相がY結線の時の電流と同様位相が\dfrac{\pi}{6}[rad]ずれるため力率にも影響します。

各負荷での電圧, 電流がわかれば電力はその総和になるだけなのでとても楽でした……。

2 V結線

V結線とは, Δ結線の起電力を1つ外したものを言います。下の図をご覧ください。たったこれだけです。
f:id:fukuro_hoho:20210216173834p:plain
ここで, a-b間の電位差は-(E_{ca}+E_{bc})となることが読み取れます。これは三相交流回路のΔ結線と同じ相電圧が生じていることを暗示しています。つまりこれは三相交流と同じ挙動を示すのです。

参考図書

お世話になった本には感謝の気持ちを忘れないように, ここに記しておきます。
・電気回路論(電気学会大学講座), 2008/5/1, 3版第1刷
・電気回路(1)直流・交流回路編, 2019/01/25 初版第35刷
この前書いたテブナンの記事と同じです。二冊目が続編になっただけかな。

最後に

だいぶ長い記事で昨日は心が折れそうでしたが, 今日の分がだいぶ簡単でびっくりしました。それなりに手抜きではあるかもしれませんが。
私の所属している学校学科のカリキュラムに三相交流回路はないのですが, よく名前を聞くし学校の教科書に大きく載ってるしやってみよ〜！っていうノリで突撃してしまいました。(明確な動機はなく, 本当に知っといたほうが良さそうだし面白そうだし, の本当のノリと勢いです。)本は2冊読んだし, Youtubeの動画も見たので間違ったことは書いていないはず……！電験III種で頻出のテーマみたいなのでネット検索してみても参考になりそうな資料がたくさん見つかりました。ありがとうございました。
この三相交流回路を通して学んだことは, 重ね合わせの理やキルヒホッフの法則を用いればだいぶいろんな回路に対応することができるということでした。能動素子が沢山入ってきたらどうなるかわからないけど。とはいえ電気回路はきっと私の知らないことでいっぱいだと思うので, これからも学ぶ体制を保ち続けていこうと思います。
ここまで読んでくださった方, 拙い文章に図でしたがありがとうございました！

電気回路 / 三相交流入門してみた(1)電力の手前まで

ふくほです。
唐突に三相交流回路について勉強する気になったので, そこでわかったことについてまとめてみます。

1 三相交流とは

同じ周波数で位相だけをずらした電源を複数組み合わせる方式を, 単相方式に対して多相方式と呼びます。三相交流は多相方式の一種で, \dfrac{2}{3}\pi[rad]ずつ位相をずらした交流電源を組み合わせています。
三相交流を用いることで, 単相と比べて送電線での電力損失を少なくできるうえ安定した電力を供給することができます。さらに簡単に生み出すことができるため, 三相交流は発電所の発電機に用いられています。

また最大値がE_m, 各周波数\omega[rad/s]の三相交流において, 3つの電源をe_a, e_b, e_cとすると, それぞれは\dfrac{2}{3}\pi[rad]の位相のずれがあるため
e_a = E_m\sin{\omega t}
e_b = E_m\sin{(\omega t -\dfrac{2}{3}\pi)}
e_c = E_m\sin{(\omega t -\dfrac{4}{3}\pi)}
と表すことができます。

2 三相交流における電源とY-Δ変換

f:id:fukuro_hoho:20210215213036p:plain
三相交流回路における電源の接続の方法として, Δ形起電力(上図右)とY形起電力(上図左)があります。Yはスターと読んだりもします。Y結線で, 図のNの部分は電位が0の点で中性点と呼ばれます。
上図で,
E_a = E_m\sin{\omega t}
E_b = E_m\sin{(\omega t -\dfrac{2}{3}\pi)}
E_c = E_m\sin{(\omega t -\dfrac{4}{3}\pi)}
としたとき, 電源をY-Δ変換をすることを考えます。
まずa-c間の電位差はY結線の場合ではE_a-E_c,Δ結線の場合ではE_{ca}と表されます。つまり, E_{ca}=E_a-E_cが成立します。これはベクトルの減算になります。E_{ab}, E_{bc}の場合も同様にすると, 次の図のようなベクトル図が書けます。E_{ab},E_{bc},E_{ca}はベクトルの減算をした後真ん中の点に平行移動しています。
f:id:fukuro_hoho:20210215213222p:plain
ここで, E_{ab},E_{bc},E_{ca}の大きさは\sqrt{3}E_mとなります。下の図をご覧ください。(私は受けたことがないのでよくわかりませんが, 電験なんかではこれが頻出だそうです。)
f:id:fukuro_hoho:20210215213234p:plain
また位相はそれぞれ\dfrac{1}{6}\pi,\dfrac{5}{6}\pi, \dfrac{3}{2}\piとなります。以上をまとめると
E_{ab} = \sqrt{3}E_m\sin{(\omega t-\dfrac{1}{6}\pi)}
E_{bc} = \sqrt{3}E_m\sin{(\omega t -\dfrac{5}{6}\pi)}
E_{ca} = \sqrt{3}E_m\sin{(\omega t -\dfrac{3}{2}\pi)}
がわかります。
Δ-Y変換の際も, ベクトル図を用いて今回の逆を行えば同じように解くことができます。また電流のY-Δ変換にも同じことができます。負荷のY-Δ変換については割愛します。

3 Δ結線とY結線

先程紹介したΔ形起電力とY形起電力はそれぞれΔ形、Y形にに接続された3つの負荷を用いてΔ結線, Y結線を構成します。その回路図を以下に示します。
f:id:fukuro_hoho:20210215213247p:plainf:id:fukuro_hoho:20210215213303p:plain
Y結線について少し詳しく書いておきます。
先程示したY結線の図において, 各負荷に流れる電流をそれぞれI_a, I_b, I_cと置きます。すべての電流はN'へ流れ入る方向であるとします。このときのI_a, I_b,I_cを, キルヒホッフの法則を使って求めてみましょう。
KVLより, 以下の3つの閉路方程式が立てられます。
E_a-E_b=Z_aI_a-Z_bI_b\tag{1}
E_b-E_c=Z_bI_b-Z_cI_c\tag{2}
E_c-E_a=Z_cI_c-Z_aI_a\tag{3}
またKCLより
I_a+I_b+I_c=0\tag{4}
が成立するので, (1)(2)(4)から成る三元一次連立方程式を解くと(1,2,3だと線形従属なので解が不定になります)クラメルの公式から
\begin{eqnarray} I_a&=& \dfrac{ \left| \begin{array}{ccc} E_a-E_b &-Z_b &0\\ E_b-E_c &Z_b&-Z_c\\ 0 &1&1 \end{array} \right| }{ \left| \begin{array}{ccc} Z_a &-Z_b &0\\ 0 &Z_b&-Z_c\\ 1 &1&1 \end{array} \right| } = \dfrac{ \left| \begin{array}{ccc} E_a-E_b &-Z_b &0\\ E_b-E_c &Z_b+Z_c&0\\ 0 &1&1 \end{array} \right| }{ \left| \begin{array}{ccc} 0 &-Z_b-Z_a &-Z_a\\ 0 &Z_b&-Z_c\\ 1 &1&1 \end{array} \right| }\\ &=&\dfrac{ (E_a-E_b)(Z_b+Z_c)+Z_b(E_b-E_c) }{ Z_aZ_b+Z_c(Z_a+Z_b) }\\ &=&\dfrac{E_a(Z_b+Z_c)-E_bZ_c-E_cZ_b}{Z_aZ_b+Z_bZ_c+Z_cZ_a} \end{eqnarray}
がわかります。ここでY_a=1/Z_a,Y_b=1/Z_b,Y_c=1/Z_cとして, 分母分子を Z_aZ_bZ_cで割ってみると
\begin{eqnarray} I_a &=&\dfrac{E_a\dfrac{Z_b+Z_c}{ Z_aZ_bZ_c}-E_b\dfrac{Z_c}{ Z_aZ_bZ_c}-E_c\dfrac{Z_b}{ Z_aZ_bZ_c}}{\dfrac{Z_aZ_b+Z_bZ_c+Z_cZ_a}{ Z_aZ_bZ_c}}\\ &=&\dfrac{E_a(Y_b+Y_c)-E_bY_b-E_cY_c}{Y_a+Y_b+Y_c}Y_a \end{eqnarray}
となり, 簡潔に表すことができました。
I_b,I_cも同様にすると
I_b=\dfrac{E_b(Y_c+Y_a)-E_cY_c-E_aY_a}{Y_a+Y_b+Y_c}Y_b
I_c=\dfrac{E_c(Y_a+Y_b)-E_aY_a-E_bY_b}{Y_a+Y_b+Y_c}Y_c
を導くことができました。ただしこれは線路のインピーダンスは考慮していません。

次に, N'での電位V_Nについて考えます。
V_N=E_a-Z_aI_a=E_b-Z_bI_b=E_cZ_cI_cとなるため(自明なので詳細は割愛), さっきの式を代入すると
\begin{eqnarray} V_N &=&E_a-Z_aI_a\\ &=&E_a-Z_a\cdot\dfrac{E_a(Y_b+Y_c)-E_bY_b-E_cY_c}{Y_a+Y_b+Y_c}Y_a\\ &=&E_a-\dfrac{E_a(Y_b+Y_c)-E_bY_b-E_cY_c}{Y_a+Y_b+Y_c}\\ &=&\dfrac{E_aY_a+E_bY_b+E_bY_c}{Y_a+Y_b+Y_c} \end{eqnarray}
Y_a=Y_b=Y_cのとき, E_a+E_b+E_c=0よりV_N=0となることがこの式から読み取ることができます。つまり, 3つの負荷のインピーダンスがすべて同じな場合は, N-N'は同電位(GND)であるので導線で接続しても回路には何も影響がないんですね。この線は中性線と呼ばれ, 回路計算で重要な役割を果たします。(中性線で区切って回路を分離することができます。)

電気回路 / 影像パラメータを見つめる

ふくほです。
二端子回路対における影像パラメータの理解がなんとなくできた気がするので, 忘れないうちにまとめておこうと思います。
一応, 大雑把にですがFパラメータの導入から書きます。この概念はフィルタ設計で重要になるのでしっかり押さえておきたいです…。

1 Fパラメータ

1.1 Fパラメータとは

f:id:fukuro_hoho:20210209171133p:plain
画像のように, 入力側にV_1, I_1, 出力側にV_2, I_2が置かれた二端子回路対を考えます。電流, 電圧の向きは図の通りです。
このとき
\left( \begin{array}{c} V_1 \\ I_1 \end{array} \right) = \left( \begin{array}{cc} A & B\\ C & D \end{array} \right) \left( \begin{array}{c} V_2 \\ I_2 \end{array} \right) \tag{1}
と表した時, A, B, C, DをFパラメータ(基本パラメータ, 伝送パラメータ, 四端子定数, 継続行列)と呼びます。このパラメータを考えることで, 様々な回路の性質を見ることができます。

1.2. Fパラメータの求め方

先程の行列をふたつの式で表すと
V_1 = AV_2 + BI_2
I_1 = CV_2 + DI_2
と書けます。よって
AはI_2=0としたときの \dfrac{V_1}{V_2}
BはV_2=0としたときの \dfrac{V_1}{I_2}
CはI_2=0としたときの \dfrac{I_1}{V_2}
DはV_2=0としたときの \dfrac{I_1}{I_2}
と考えるとそれぞれのパラメータを求めることができます。
電圧を0とするときはその端子を短絡, 電流を0とするときはその端子を開放してやるとよいです。
Fパラメータの場合開放・短絡するのは出力側の端子だけでよいですね。

また, 相反二端子回路対では\det{F}=1となります。つまりA, B, C, Dのうち3つが決まればもう1つは計算によって求められるのです。
めちゃくちゃ大雑把ですがパラメータについてはここまでにしておきます…

2 影像パラメータ

2.1 影像インピーダンス

f:id:fukuro_hoho:20210209175617p:plain
上の図のように, 端子2-2'にZ_{02}を接続したときに端子1-1'からみたインピーダンスがZ_{01}, 端子1-1'にZ_{01}を接続したときに端子2-2'からみたインピーダンスがZ_{02}であるようにしたとき, Z_{01}, Z_{02}を影像インピーダンスと呼びます。それぞれのインピーダンスが鏡の影像のような関係にあるからこう呼ぶんだとか。
では, 影像インピーダンスを求めていきます。
オームの法則から, 影像インピーダンスはそれぞれ
Z_{01}=\dfrac{V_1}{I_1}
Z_{02}=\dfrac{V_2}{I_2}
と書けます。次に V_1, I_1をFパラメータで表した形に変形してみます。
Z_{01}=\dfrac{AV_2 + BI_2}{CV_2 + DI_2}
次にV_2=Z_{02}I_2であるので
\begin{eqnarray*} Z_{01} &=&\dfrac{A (Z_{02}I_2) + BI_2}{C(Z_{02}I_2) + DI_2}\\ &=&\dfrac{AZ_{02}+B}{CZ_{02}+D}\tag{2} \end{eqnarray*}
が成立することがわかります。
また(1)式の両辺に,左からFパラメータの逆行列をかけてあげると \det{F}=1より
\left( \begin{array}{c} V_2 \\ I_2 \end{array} \right) = \left( \begin{array}{cc} D & {-B}\\ {-C} & A \end{array} \right) \left( \begin{array}{c} V_1 \\ I_1 \end{array} \right)
となります。先程と同様にしてみます。
V_2 = DV_1 -BI_1
I_2 =-CV_1 +AI_1

また, 右側の端子を入力としたときは電流の向きが入れ替わるため
V_{1}=-Z_{01}I_1
とマイナスがつくことに注意します。

\begin{eqnarray*} Z_{02} &=&\dfrac{V_2}{I_2}\\ &=&\dfrac{DV_1 -BI_1}{-CV_1 +AI_1}\\ &=&\dfrac{D(-Z_{01}I_1) -BI_1}{-C(-Z_{01}I_1) +AI_1}\\ &=&\dfrac{DZ_{01}+B}{CZ_{01}+A}\tag{3} \end{eqnarray*}

(2)(3)式から
CZ_{01}Z_{02}+DZ_{01}=AZ_{02}+B
CZ_{01}Z_{02}+AZ_{02}=DZ_{01}+B
が得られます。
二式の和を取ると
2CZ_{01}Z_{02}=2B
Z_{01}Z_{02}=\dfrac{B}{C}
次に二式の差を取ると
DZ_{01}-AZ_{02}=AZ_{02}-DZ_{01}
\dfrac{Z_{01}}{Z_{02}}=\dfrac{A}{D}
が得られます！ここから
Z_{01}=\sqrt{\dfrac{AB}{CD}}, Z_{02}=\sqrt{\dfrac{BD}{AC}}
と求めることができました。
またFパラメータが対称行列である場合A=Dであるため
Z_{01}=Z_{02}=\sqrt{\dfrac{B}{D}}
となります。
ここでは負の影像インピーダンスは考えないものとしています。

2.2 伝達定数

私はここの理解に苦労しました。
よし頑張るぞ。
先程の図の端子 2-2'にZ_{02}を接続したときのV_1と V_2の比を e^{\theta_1}と置きます。(これは短絡して電流を０としていないため, 影像パラメータのAとは異なります。)影像パラメータを用いて式を変形してみます。
\begin{eqnarray*} e^{\theta_1} &=& \dfrac{V_1}{V_2}\\ &=&\dfrac{AV_2+BI_2}{V_2}\\ &=&(A+B\dfrac{I_2}{V_2})V_2\\ &=&(A+\dfrac{B}{Z_{02}})V_2\\ &=&(A+\dfrac{B}{\sqrt{\dfrac{BD}{AC}}})V_2\\ &=&\sqrt{\dfrac{A}{D}}(\sqrt{AD}+\sqrt{BC}) \end{eqnarray*}
電流でも同様に, I_1と I_2の比を e^{\theta_2}と置いて計算すると
e^{\theta_2}=\sqrt{\dfrac{D}{A}}(\sqrt{AD}+\sqrt{BC})
が導かれます。
伝達係数は, この\theta_1と\theta_2の相加平均, \dfrac{\theta_1+\theta_2}{2}を取ります。
\begin{eqnarray} e^{\theta_1+\theta_2} &=&\sqrt{ \dfrac{A}{D} }( \sqrt{AD}+\sqrt{BC} ) \times \sqrt{ \dfrac{D}{A} } (\sqrt{AD}+\sqrt{BC})\\ &=&(\sqrt{AD}+\sqrt{BC})^{2} \end{eqnarray}
両辺の自然対数を取って
\theta_1+\theta_2=2\ln{(\sqrt{AD}+\sqrt{BC})}\\ \therefore \dfrac{\theta_1+\theta_2}{2}=\ln{(\sqrt{AD}+\sqrt{BC})}
この \thetaとZ_{01}, Z_{02}をまとめて影像パラメータと呼んでいます。
また\thetaは実数とは限りません。\theta = \alpha +j\betaと表すと\alphaを減衰定数, \betaを位相定数と呼びます。
また端子1-1'での電力を W_1, 端子2-2'での電力をW_2とすると, 定義から
\alpha+j\beta =\ln{\sqrt{\dfrac{V_1I_1}{V_2I_2}}}=-\ln{\sqrt{\dfrac{V_2I_2}{V_1I_1}}}=-\ln{\sqrt{\dfrac{W_2}{W_1}}}
と表すこともできます。つまり\alphaによって入力と出力の電力の比を得ることができるのです。
任意の\betaにおいて|e^\beta|=1であるので, \betaは電力比を求めるうえでは貢献しません。その代わり, e^{j\beta}=\cos\beta+j\sin\betaであるため, この\betaが位相定数と呼ばれるのも納得がいくと思います。
また出力が入力に対して減衰していないとき,
|\dfrac{W_2}{W_1}|=1
が得られます。
e^{\alpha +j\beta}= \dfrac{W_1}{W_2}\\
両辺の絶対値を取って整理すると
\begin{eqnarray} e^{\alpha}&=&1\\ \alpha&=&0 \end{eqnarray}
を得ることができます。
したがってFパラメータを用いると

これはフィルタ(LPF, HPFなど)を設計するうえで重要な概念になります。

最後に

最後, ごちゃごちゃになってしまった…
とりあえずこれで終わりますが、また書き直すと思います
近いうちにフィルタの記事も書きます(決意)。

参考図書

お世話になった本には感謝の気持ちを忘れないように, ここに記しておきます。
・電気回路論(電気学会大学講座), 2008/5/1, 3版第1刷
・電気回路(2)回路網・過渡現象編, 2019/01/25 初版第30刷
この前書いたテブナンの記事と同じです。二冊目が続編になっただけかな。